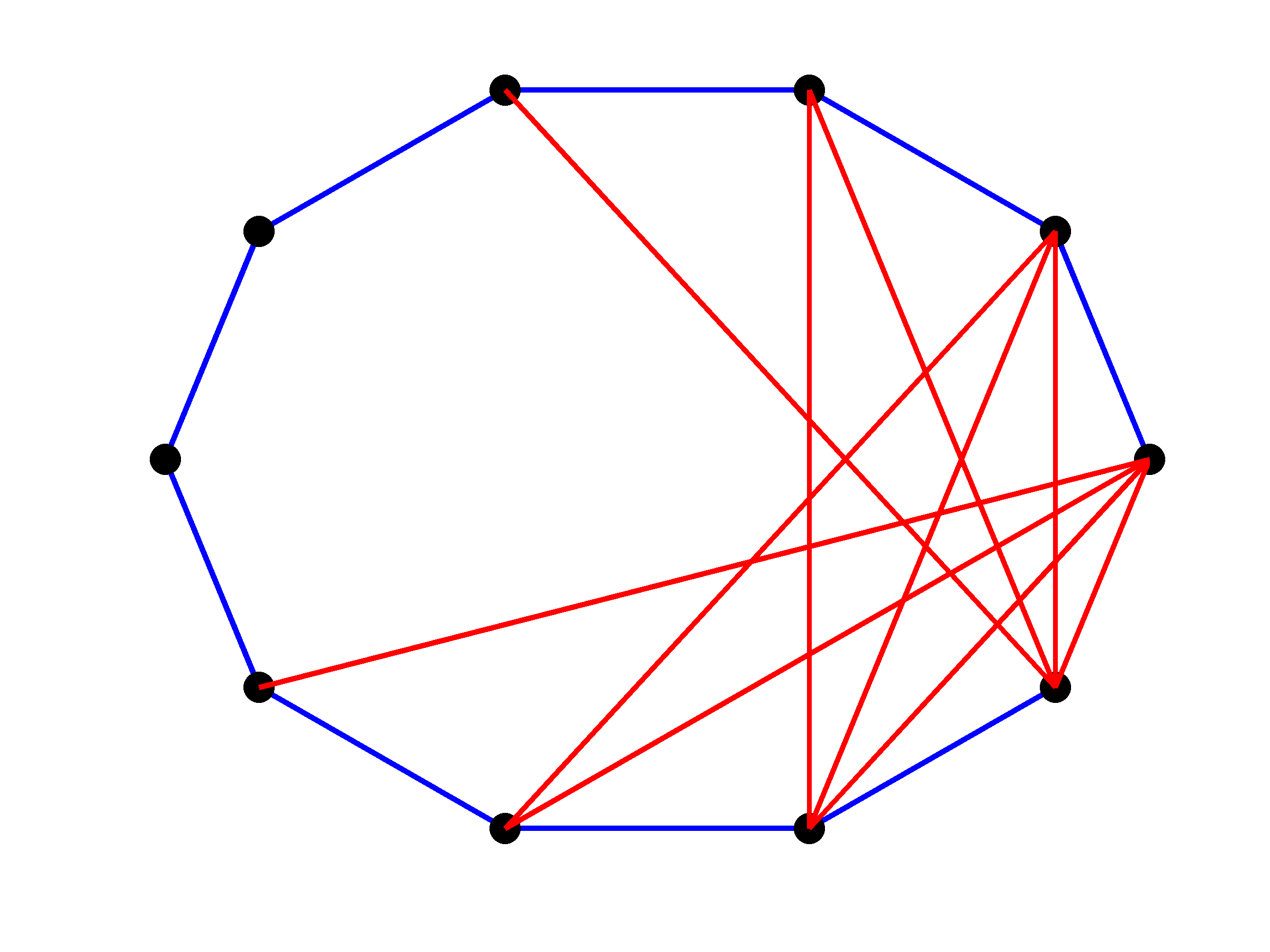
Path plant network
We employ our customized algorithm using graphsp_IP_res.m to grow a
resistive path network with  nodes. We set
nodes. We set  and choose the state
weight that penalizes the mean-square deviation from the network average,
and choose the state
weight that penalizes the mean-square deviation from the network average,
 .
.
As shown below, for  , we obtain a centralized controller that
requires information exchange between all nodes. As
, we obtain a centralized controller that
requires information exchange between all nodes. As  increases, the
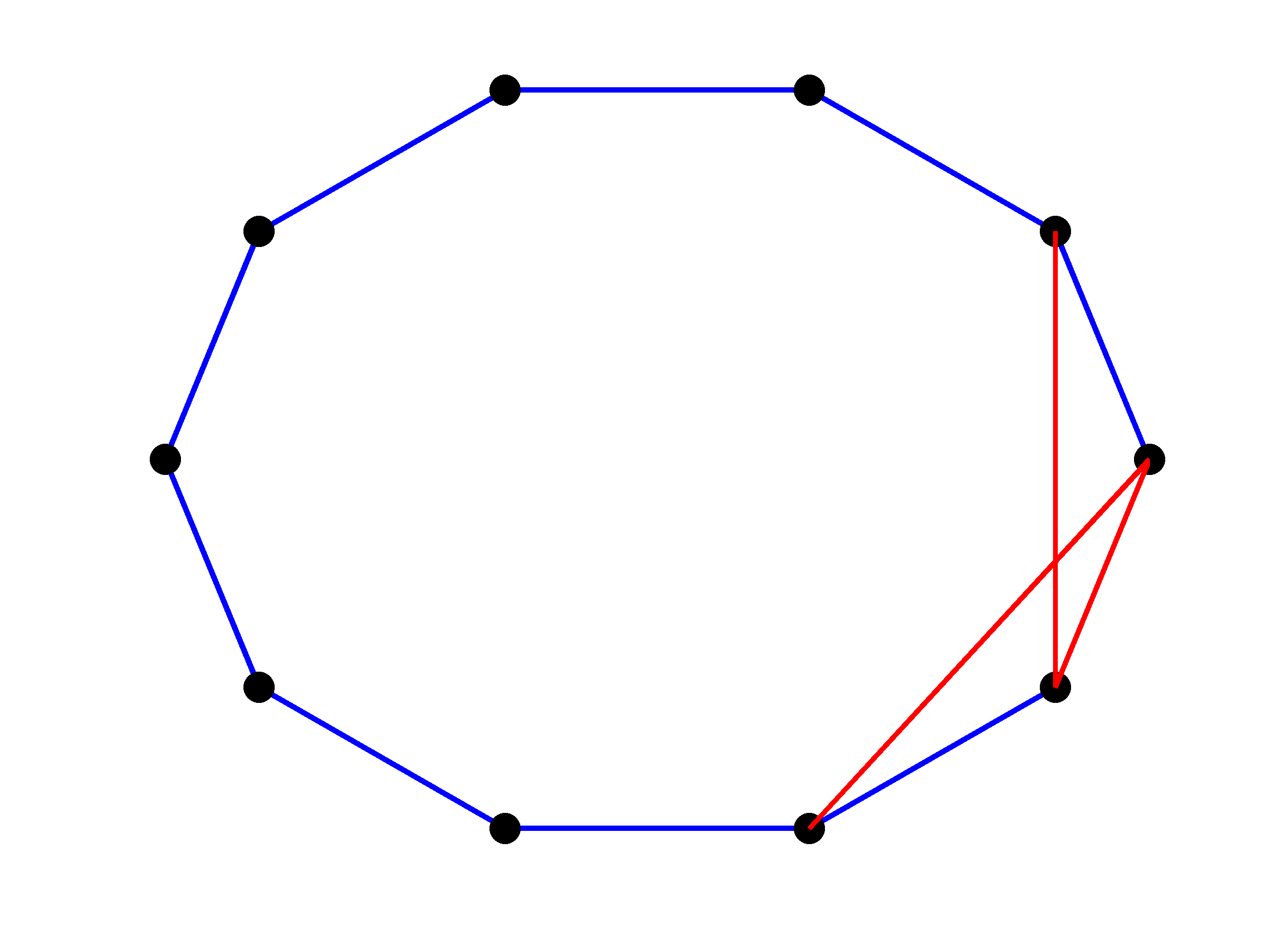
number of added edges gradually decreases. Finally, for
increases, the
number of added edges gradually decreases. Finally, for  , a single edge is added and this edge generates the longest
cycle. This is in agreement with recent theoretical developments of
Zelazo, Schuler, and
Allgower ’13 where it was shown that the longest cycle is most beneficial
for improving the
, a single edge is added and this edge generates the longest
cycle. This is in agreement with recent theoretical developments of
Zelazo, Schuler, and
Allgower ’13 where it was shown that the longest cycle is most beneficial
for improving the  performance of tree networks.
performance of tree networks.
Blue lines identify edges in the plant graph; red lines identify edges in
the controller graph;  identifies the value of the
regularization parameter
identifies the value of the
regularization parameter  for which all edge weights in the
controller graph are equal to zero.
for which all edge weights in the
controller graph are equal to zero.
 |
|
 |
|
 |
|
 |
|



